Dauerlinien für die Hoch- und Niedrigwasserstatistik
Dies ist die vierte und letzte Übung aus einer Reihe von Übungen zu hydrologisch/metereologischen Datensätzen und deren Auswertung. Sie setzt die Übung zu Empirischen Verteilungsfunktionen fort.
Einleitung
In dieser Übung sollen Dauerlinien (= empirische Verteilungsfunktionen) für die Hochwasserstatistik und die Niedrigewasserstatistik gezeichnet werden. Zusätzlich sollen theoretische Verteilungsfunktionen an die empirischen Verteilungen angepasst werden und über Q-Q-Plots mit diesen verglichen werden.
Anschließend soll mit der Verteilungsfunktion, die die Daten am besten beschreibt ein Wahrscheinlichkeits-Plot und ein Plot für das Wiederkehrintervall erstellt werden (hierfür ist der Code weitestgehend vorgegeben).
Diese Verteilungsfunktionen sollen angepasst werden:
- Normalverteilung
- log-Normalverteilung
- Gumbel-Verteilung
- Weibull-Verteilung
Diese Verteilungsfunktionen sind in R in den Funktionen qnorm(), qlnorm(), qgumbel() und qweibull() implementiert. Konsultieren Sie die entsprechenden Hilfe-Seiten, um mehr zu diesen Verteilungsfunktionen und die Benutzung der Funktionen zu erfahren.
Um die theoretischen Verteilungsfunktionen an die empirische Verteilung anzupassen verwenden wir die Momentenmethode: Wir berechnen die Werte für das 1. und 2. Moment der Verteilung, also für den Lage- und den Skalierungs-Parameter1 und setzen diese in die Verteilungsfunktion ein. Diese Momente sind wie folgt definiert:
| Verteilungsfunktion | 1. Moment (Lage) | 2. Moment (Skalierung) |
|---|---|---|
| Normalverteilung | mean(x) | sd(x) |
| log-Normalverteilung | mean(log(x)) | sd(log(x)) |
| Gumbel-Verteilung | mean(x)-0.5772*gscale | gscale = sqrt(6)/pi*sd(x) |
Für die Weibull-Verteilung lassen sich die Momente nicht so einfach berechnen. Hier verwenden wir das sogenannte Maximum-likelihood-Fitting zum Anpassen der Verteilungsfunktion. Diese Methode ist etwas komplizierter, ist jedoch in R schon in der Funktion fitdistr() implementiert, die wir benutzen werden.
Wir werden also wie folgt vorgehen:
- Daten herunterladen
- Daten zu hydrologischen Jahren aggregieren
- Maximum für Hochwasserstatistik
- Minimum für Niedrigwasserstatistik
- Dauerlinie (= empirische Verteilungsfunktion) zeichnen (Anleitung in letzter Übung)
- Q-Q-Plot erstellen mit
- y-Achse: Quantile der empirischen Verteilung
- x-Achse: Quantile der theoretischen Verteilung
Daten herunterladen
Wir werden die Funktion get_usgs_gage() aus dem Package EcoHydRology verwenden, um Abflussdaten vom Server waterdata.usgs.gov des USGS (United States Geological Survey) herunterzuladen. Falls dies noch nicht installiert ist bitte den Befehl install.packages("EcoHydRology") vorher ausführen.
library("EcoHydRology")
help(get_usgs_gage)
Licking_River = get_usgs_gage(flowgage_id="03253500", begin_date="1928-10-01", end_date="2014-09-30")Die heruntergeladenen Daten haben folgende Struktur:
str(Licking_River)## List of 6
## $ declat : num 38.7
## $ declon : num -84.3
## $ flowdata:'data.frame': 31044 obs. of 6 variables:
## ..$ agency : chr [1:31044] "USGS" "USGS" "USGS" "USGS" ...
## ..$ site_no: num [1:31044] 3253500 3253500 3253500 3253500 3253500 ...
## ..$ date : chr [1:31044] "1928-10-01" "1928-10-02" "1928-10-03" "1928-10-04" ...
## ..$ flow : num [1:31044] 251997 256890 256890 256890 244658 ...
## ..$ quality: chr [1:31044] "A" "A" "A" "A" ...
## ..$ mdate : Date[1:31044], format: "1928-10-01" ...
## ..- attr(*, "na.action")=Class 'omit' Named int [1:392] 18263 18264 29221 29222 29223 29224 29225 29226 29227 29228 ...
## .. .. ..- attr(*, "names")= chr [1:392] "18263" "18264" "29221" "29222" ...
## $ area : num 8448
## $ elev : num 236
## $ gagename: chr "LICKING RIVER AT CATAWBA, KY"Die eigentliche Abflussdaten sind in einem data.frame unter Licking_River$flowdata gespeichert. Schauen wir uns diesen data.frame an:
View(Licking_River$flowdata)| agency | site_no | date | flow | quality | mdate |
|---|---|---|---|---|---|
| USGS | 3253500 | 1928-10-01 | 251997.3 | A | 1928-10-01 |
| USGS | 3253500 | 1928-10-02 | 256890.4 | A | 1928-10-02 |
| USGS | 3253500 | 1928-10-03 | 256890.4 | A | 1928-10-03 |
| USGS | 3253500 | 1928-10-04 | 256890.4 | A | 1928-10-04 |
| USGS | 3253500 | 1928-10-05 | 244657.6 | A | 1928-10-05 |
| USGS | 3253500 | 1928-10-06 | 229978.1 | A | 1928-10-06 |
Es gibt zwei Datums-Spalten. Aus der Struktur erkennen wir, dass die erste Datums-Spalte date ein Character-Vektor ist. Die zweite Spalte mdate ist in einem Datums-Format. Also werden wir diese später verwenden. Mit Licking_river$flowdata$flow können wir die Abflussdaten abrufen.
Plotten wir z.B. eine Zeitreihe der Daten:
plot(flow~mdate, data=Licking_River$flowdata, type="l", xlab="Zeit", ylab="Abfluss")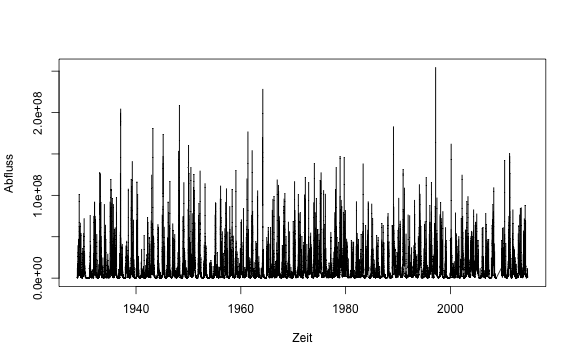
Hochwasserstatistik
Für die Hochwasserstatistik brauchen wir das jährliche Abflussmaximum. Um dieses zu berechnen aggregieren wir die täglichen Daten zu jährlichen Daten über die Funktion max. Für die Aggregierung steht uns die Funktion aggregate zur Verfügung. Da wir über das hydrologische Jahr aggregieren möchten, müssen wir dieses zuerst noch berechnen. Das Hydrologische Jahr, wie es der USGS definiert beginnt für dieses Gebiet am 1. Oktober und endet am 30. September. Wenn wir also 3 Monate zu mdate dazu rechnen und dann mit year() das Datum abfragen, werden die Monate Oktober bis Dezember jeweils dem nächsten Jahr zugeordnet. Wir speichern das Ergebnis dieser Abfrage in einer neuen Spalte namens hydroYear im flowdata data.frame. Die Funktionen year() und months() entstammen aus dem lubridate package, das deshalb vorher geladen werden muss.
library(lubridate)
Licking_River$flowdata$hydroYear <- year(Licking_River$flowdata$mdate + months(3))Zum Aggregieren übergeben wir der Funktion aggregate unsere Abflussdaten, das by= Argument, anhand dessen die Daten aggregiert werden sollen (in unserem Falle das hydrologische Jahr) und mit FUN die Funktion mit der die Daten aggregiert werden sollen.
annual_max <- aggregate(Licking_River$flowdata$flow, by = list(Licking_River$flowdata$hydroYear), FUN=max)$xaggregate gibt standardmäßig den Aggregationsparameter als zusätzliche Spalte zurück. Daher verwenden wir $x, um nur die Spalte mit den aggregierten Werten unter annual_max zu speichern.
Wir sehen, dass die Daten nun deutlich anders verteilt sind:
plot(annual_max, type="l")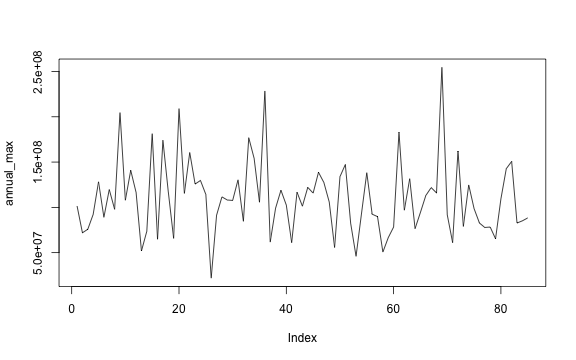
Dauerlinie
Die Dauerlinie bzw. empirische Verteilungsfunktion zeichnen wir wie in der letzten Übung gezeigt:
data_sorted <- sort(annual_max)
n <- length(annual_max) # n equals the number of entries
i <- 1:n # the running index of the entries
p_i <- (i - 0.4)/(n + 0.2) # the plotting position with a=0.4 (see the USGS book)
plot( x=data_sorted, y=p_i, type="l", xlab="Abfluss", ylab="Quantile", main=paste("Dauerlinie", Licking_River$gagename))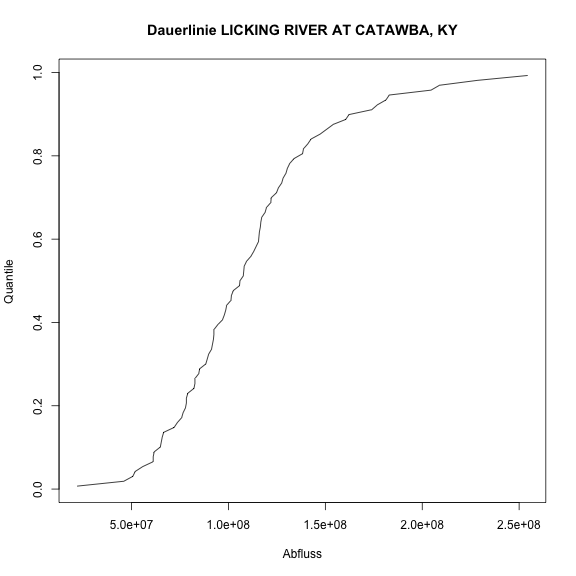
Verteilungsfunktion anpassen
Für die Hochwasserstatistik wollen wir die theoretischen Verteilungsfunktionen der Normalverteilung, log-Normalverteilung und Gumbel-Verteilung an unsere Daten anpassen. Wie in der Einleitung beschrieben wollen wir das über die Momentenmethode realisieren. Zur Wiederholung hier die tabelle für die Berechung der Momente:
| Verteilungsfunktion | 1. Moment (Lage) | 2. Moment (Skalierung) |
|---|---|---|
| Normalverteilung | mean(x) | sd(x) |
| log-Normalverteilung | mean(log(x)) | sd(log(x)) |
| Gumbel-Verteilung | mean(x)-0.5772*gscale | gscale = sqrt(6)/pi*sd(x) |
Es folgt ein Beispiel, wie dies für die Normalverteilung in R umgesetzt werden kann. Bitte schreiben Sie entsprechenden Programmcode für die log-Normalverteilung (qlnorm()) und die Gumbel-Verteilung (qgumbel()). Speichern Sie diese unter log_normal und gumbel und zeichnen Sie diese mit zusätzlichen Linien in die Grafik ein.
Die Gumbel-Funktion ist nicht im Basispaket von R implementiert. Daher müssen wir noch das Paket evd hinzuladen. Falls dieses noch nicht installiert ist, kann es mit install.packages("evd") installiert werden.
library("evd")#---- Normalverteilung anpassen ----
norm_location <- mean(annual_max)
norm_scale <- sd(annual_max)
normal <- qnorm(p = p_i, mean = norm_location, sd = norm_scale)
#---- log-Normalverteilung anpassen ----
log_normal <- qlnorm(p_i, meanlog=mean(log(annual_max)), sdlog=sd(log(annual_max)))
#---- Gumbel-Verteilung anpassen ----
gscale <- sqrt(6)/pi*sd(annual_max)
gloc <- mean(annual_max)-0.5772*gscale
gumbel <- qgumbel(p_i, loc=gloc, scale=gscale)plot( x=data_sorted, y=p_i, type="l", xlab="Abfluss", ylab="Quantile", main=paste("Dauerlinie", Licking_River$gagename))
lines(normal, p_i, col="green")
lines(log_normal, p_i, col="orange")
lines(x=gumbel, y=p_i, col="blue")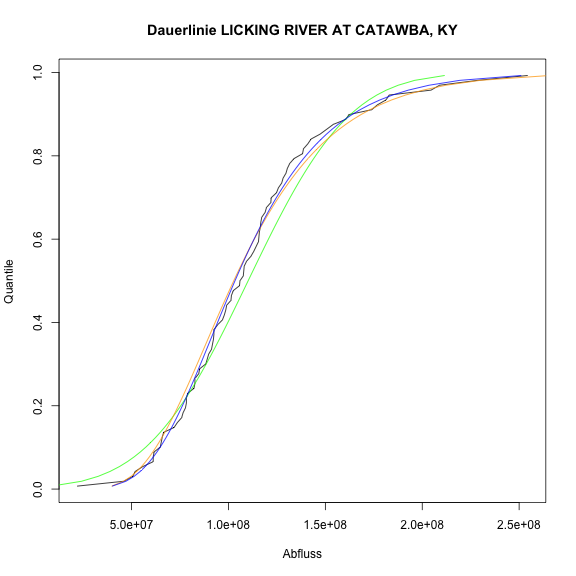
Q-Q-Plots zur Bewertung der Anpassung
Zur Überprüfung und Bewertung der Anpassung stellen wir die Quantile der empirischen Verteilung denen der angepassten theoretischen Verteilung gegenüber. Dies nennt sich ein Q-Q-Plot: auf die Y-Achse zeichnen wir die Quantile der empirischen Verteilung (data_sorted). Auf die X-Achse zeichen wir die Quantile mit gleicher Wahrscheinlichkeit, die wir über die angepasste Verteilungsfunktion berechnet haben (z.B. normal oder gumbel). Um die Werte auf den Achsen festzusetzen und für alle Grafiken gleich zu halten berechnen wir mit range(annual_max) die Spanne unserer Werte.
Anschließend plotten wir noch eine 1:1-Linie in die Grafik mit dem Befehl abline(a=0, b=1). Weichen unsere Punte von dieser Linie ab, bedeutet dies eine schlechte Anpassung bzw. geringe Übereinstimmung der theoretischen Verteilung mit der empirischen.
range <- range(annual_max)
title <- "Theoretical and empirical quantiles (Q-Q-Plot)"
plot(normal, data_sorted, xlim=range, ylim=range, main=title)
abline(a=0, b=1)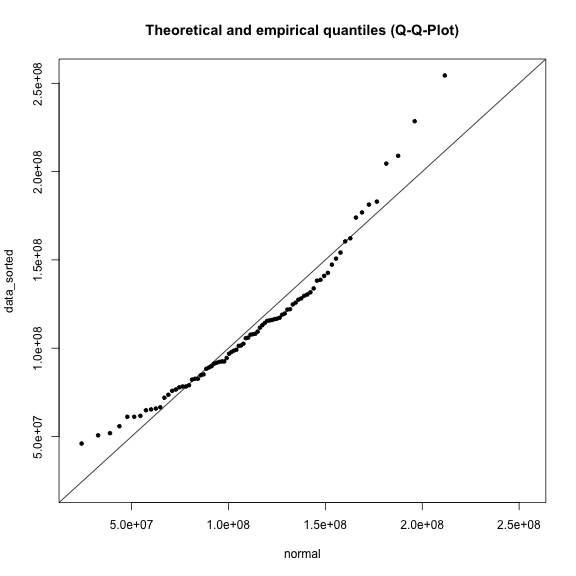
Erstellen Sie zwei weitere Q-Q-Plots for die log-Normalverteilung und die Gumbel-Verteilung. Welche der Verteilungen zeigt die geringsten Abweichungen zur 1:1-Linie?
plot(log_normal, data_sorted, xlim=range, ylim=range, main=title)
abline(a=0, b=1)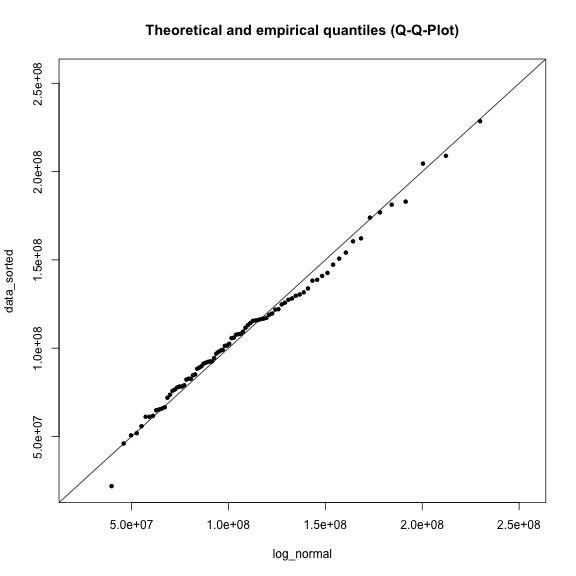
plot(gumbel, data_sorted, xlim=range, ylim=range, main=title)
abline(a=0, b=1)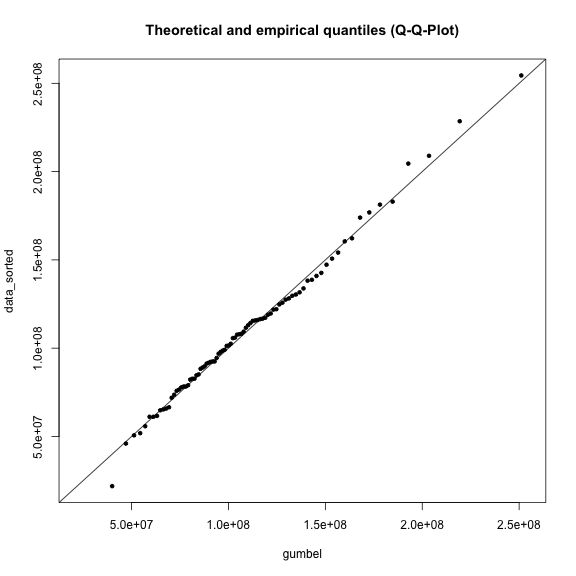
Wahrscheinlichkeitsplots und Wiederkehrintervall
Im folgenden wird gezeigt, wie man einen Wahrscheinlichkeitsplot und das Wiederkehrintervall darstellt. Hier werden dem Q-Q-Plot lediglich weitere Achsen hinzugefügt, die sich an den theoretischen Wahrscheinlichkeiten bzw. dem Wiederkehrintervall orientieren. Außerdem sind vertikale Lininen eingezeichnet, um das Ablesen von Wahrscheinlichkeiten bzw. Wiederkehrintervallen zu erleichtern. Ein Plot mit einer solchen Achseneinteilung wird auch Wahrscheinlichkeitsnetz genannt und dient Ihnen in ihrem Extremwertbeleg zum manuellen Anpassen einer Verteilungsfunktion und damit zum manuellen Extrapolieren von Wiederkehrintervallen.
Die Position zum Einzeichnen der Wahrscheinlichkeiten \(p_i\) muss über die Gumbel-Funktion berechnet werden. Daher wird hier tick_pos <- qgumbel(tick_lab/100, gloc, gscale) verwendet, um aus dem Array tick_lab die Position tick_pos zum Einzeichnen zu berechnen.
Das Wiederkehrintervall \(T(x)\) berechnet sich aus der Unterschreitungswahrscheinlichkeit \(p_{un}\) mit der Formel:
\[T(x)=\frac{100}{100-p_{un}}\]Und entsprechend aus der Überschreitungwahrscheinlichkeit \(p_{üb}\) mit:
\[T(x) = \frac{100}{p_{üb}}\]#--------- Probability plot -------------------
par(mar=c(5,5,9,1))
# probabilities in percentage to draw lines at
grid_lines <- c(seq(0.01, 0.1, 0.01), seq(0.1,1,0.1), 1:10, seq(10,90,10), seq(90,99,1), seq(99, 99.9, 0.1), seq(99.9, 99.99, 0.001))
# probabilities for axis labeling
tick_lab <- c(0.01, 0.1, 0.5, 1, 10, 50, 90, 99, 99.5, 99.9, 99.99 )
theoretical_quantiles <- qgumbel(p_i, gloc, gscale)
grid_pos <- qgumbel(grid_lines/100, gloc, gscale)
tick_pos <- qgumbel(tick_lab/100, gloc, gscale)
#---- probability of being higher than specified value ----
plot(theoretical_quantiles, data_sorted, pch=20, axes=T, lab=c(10,10,7), xlab="theoretische Verteilung", ylab="empirische Verteilung", panel.first={
grid(NA,NULL, lwd=1)
abline(a=0, b=1)
abline(v=grid_pos, lty=3, lwd=1)
abline(v=tick_pos, lwd=1)
})
# Achsenbeschriftung Wahrscheinlichkeit
axis(3, tick_pos, 100-tick_lab, las=3)
title(main="Wahrscheinlichkeit in %, dass Abfluss größer ist", cex.main=1, font.main=1, line=2.5)
# Achsenbeschriftung Wiederkehrintervall
axis(3, tick_pos, round(100/((100-tick_lab)),3), las=3, line=4.5)
title(main="Wiederkehrintervall in Jahren", cex.main=1, font.main=1, line=7)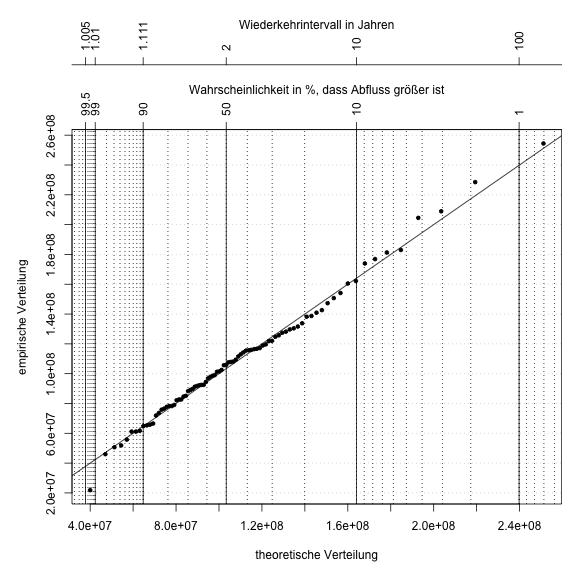
Beispiel für ein Extremwertwahrscheinlichkeitsnetz zur manuellen Extrapolation von Extremwertereignissen.
Niedrigewasserstatistik
Um die Niedrigwasserstatistik zu berechnen, ist der erste Schritt wieder die jährliche Aggregierung. Verwenden Sie wie in der Hochwasserstatistik die Funktion aggregate um diesmal annual_min zu berechnen (Tipp: übergeben Sie dazu min als Argument für FUN).
Für die Niedrigwasserstatistik werden wir eine zusätzliche Verteilungfsunktion anpassen: die Weibull-Verteilung. Diese können wir nicht über die Momentenmethode anpassen, sondern nur über die Maximum-likelihood-Methode. Dies kann in R mit der Funktion fitdistr() aus dem MASS-Paket auf die folgende Weise gemacht werden:
#---- Weibull Verteilung anpassen ----
library("MASS")
parameter <- fitdistr(annual_min, "weibull")
wshape <- parameter$estimate["shape"]
wscale <- parameter$estimate["scale"]
weibull <- qweibull(p_i, shape=wshape, scale=wscale)
lines(weibull, p_i, col="red")Erstellen Sie analog zur Hochwasserstatistik eine Grafik, die die empirische Verteilungsfunktion sowie vier weitere Linien für die vier angepassten Verteilungsfunktionen enthält. Für die Niedrigwasserstatistik empfiehlt es sich in der plot-Funktion das zusätzliche Argument log="x" zu verwenden, um die x-Achse logarithmisch darzustellen. Auf diese Weise erkennt man im unteren Wertebereich mehr Details.
Daraufhin plotten Sie auch hier für jede angepasste Verteilungsfunktion einen Q-Q-Plot mit den empirischen Daten.
Welche Verteilungsfunktion liefert hier die beste Anpassung?
#---- get the annual min: ----
annual_min <- aggregate(Licking_River$flowdata$flow, by = list(Licking_River$flowdata$hydroYear), FUN=min)$x
#---- prepare quantile plot ----
data_sorted <- sort(annual_min)
n <- length(annual_min) # n equals the number of entries
i <- 1:n # the running index of the entries
p_i <- (i - 0.4)/(n + 0.2) # the plotting position with a=0.4 (see the USGS book)library("MASS")
#---- normal distribution ----
normal <- qnorm(p_i, mean(annual_min), sd(annual_min))
#---- log-normal distribution ----
log_normal <- qlnorm(p_i, meanlog=mean(log(annual_min)), sdlog=sd(log(annual_min)))
#---- Gumbel distribution ----
gscale <- sqrt(6)/pi*sd(annual_min)
gloc <- mean(annual_min)-0.5772*gscale
gumbel <- qgumbel(p_i, loc=gloc, scale=gscale)
#---- Weibull distribution ----
parameter <- fitdistr(annual_min, "weibull")
wshape <- parameter$estimate["shape"]
wscale <- parameter$estimate["scale"]
weibull <- qweibull(p_i, shape=wshape, scale=wscale)plot( x=data_sorted, y=p_i, type="l", xlab="discharge", ylab="quantile", panel.first=grid(), log="x", main="Quantile plot")
lines(normal, p_i, col="green")
lines(log_normal, p_i, col="orange")
lines(x=gumbel, y=p_i, col="blue")
lines(weibull, p_i, col="red")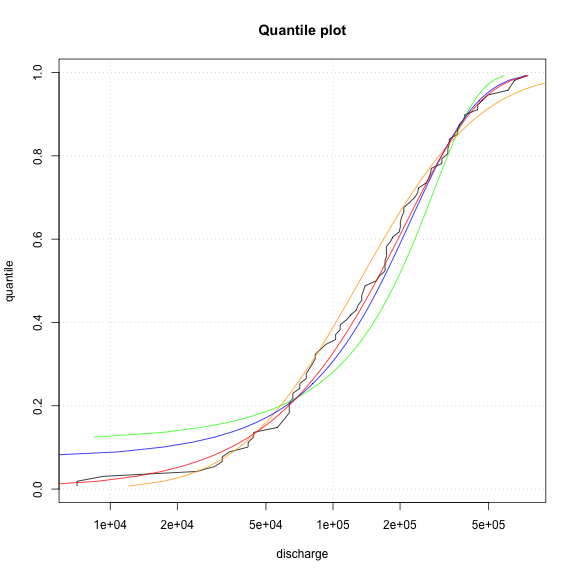
range <- range(annual_min,1)
title <- "Theoretical and empirical quantiles (Q-Q-Plot)"
plot(normal, data_sorted, xlim=range, ylim=range, main=title)
abline(a=0, b=1)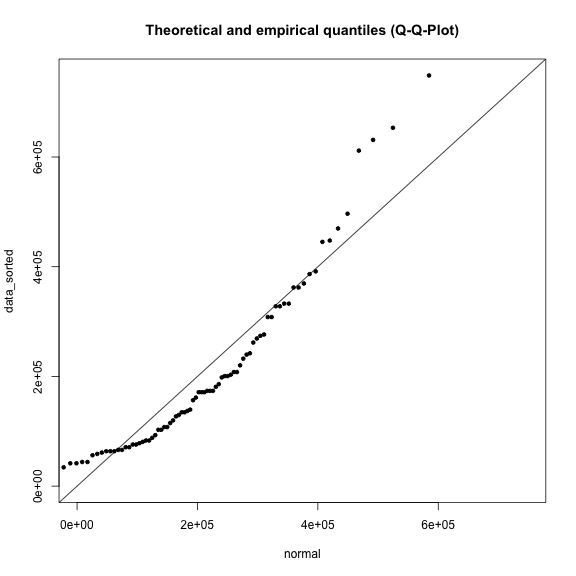
plot(log_normal, data_sorted, xlim=range, ylim=range, main=title)
abline(a=0, b=1)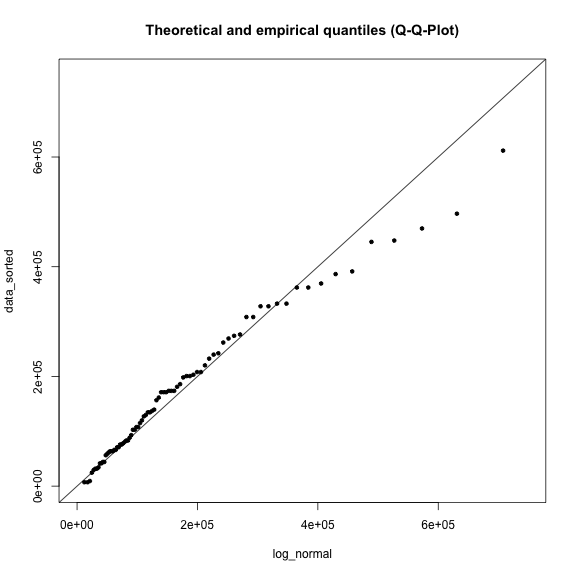
plot(weibull, data_sorted, xlim=range, ylim=range, main=title)
abline(a=0, b=1)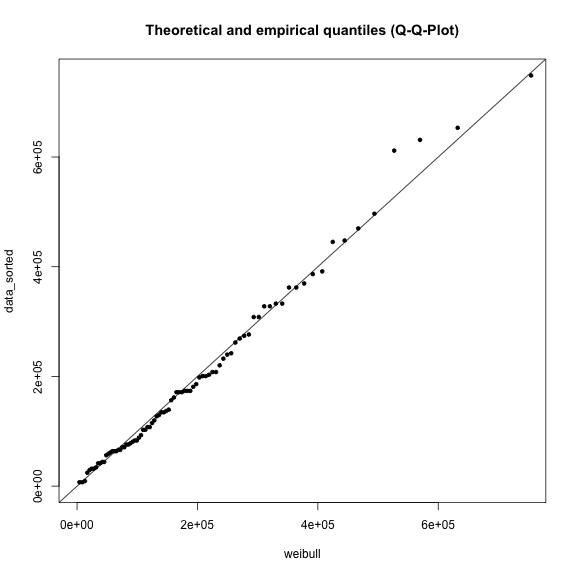
Wahrscheinlichkeitsplot und Wiederkehrintervall
Auch hier können wir wieder ein Wahrscheinlichkeitsplot mit Wiederkehrintervall zeichnen. Für die Niedrigwasserstatistik macht es mehr Sinn, die Unterschreitungswahrscheinlichkeit darzustellen.
par(mar=c(5,5,9,1))
# probabilities in percentage to draw lines at
grid_lines <- c(1:10, seq(10,90,10), seq(90,99,1), seq(99, 99.9, 0.1), seq(99.9, 99.99, 0.001))
# probabilities for axis labeling
tick_lab <- c(1, 10, 50, 90, 99, 99.5, 99.9, 99.99 )
theoretical_quantiles <- qweibull(p_i, shape=wshape, scale=wscale)
grid_pos <- qweibull(grid_lines/100, wshape, wscale)
tick_pos <- qweibull(tick_lab/100, wshape, wscale)
plot(theoretical_quantiles, data_sorted, pch=20, axes=T, lab=c(10,10,7), xlab="theoretische Verteilung", ylab="empirische Verteilung", panel.first={
grid(NA,NULL, lwd=1)
abline(a=0, b=1)
abline(v=grid_pos, lty=3, lwd=1)
abline(v=tick_pos, lwd=1)
})
# Achsenbeschriftung Wahrscheinlichkeit
axis(3, tick_pos, tick_lab, las=3)
title(main="Wahrscheinlichkeit in %, dass Abfluss kleiner ist", cex.main=1, font.main=1, line=2.5)
# Achsenbeschrifgunt Wiederkehrintervall
axis(3, tick_pos, round(100/tick_lab,3), las=3, line=4.5)
title(main="Wiederkehrintervall in Jahren", cex.main=1, font.main=1, line=8)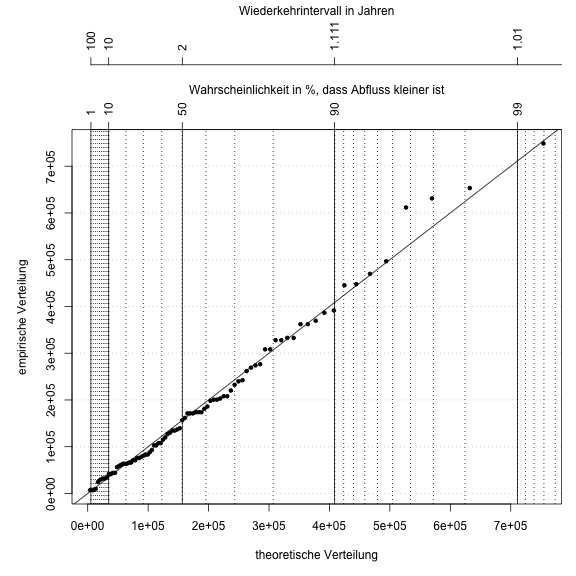
-
Andere Verteilungen haben zusätzlich noch einen 3. Moment, der die Schiefe beschreibt und wiederum andere Verteilungen haben sogar noch weitere Momente. ↩